Extending MXFP4 and NVFP4 with Redundant Zero Remapping (RaZeR) for Accurate 4-bit LLM Quantization
TL;DR
We extend the standard FP4 format with Redundant Zero Remapping (RaZeR), which adaptively remaps the negative zero encoding to one of some pre-defined special values. This allows to maximally utilize the available quantization encodings. Through the careful algorithm-hardware co-design of these special values, RaZeR can better fit LLM numerical distributions with minimal hardware overhead. By integrating RaZeR on top of two widely used FP4 variants—MXFP4 and NVFP4—we achieve better accuracy under 4-bit weight quantization across a range of large language models (LLMs).
Introduction
The substantial memory footprint and computational demand of LLMs present critical challenges for efficient inference. Recent advancements in quantization alleviate the memory bottleneck of LLMs while boosting the computational throughput. Specifically, 4-bit weight-only quantization offers a favorable trade-off between model accuracy and hardware performance, and can be effectively performed in a post-training manner. Motivated by this, the industry has adopted two custom 4-bit data types—MXFP4 and NVFP4—both based on the standard FP4 format, for LLM quantization. For instance, the recently released GPT-OSS is natively quantized to MXFP4 through quantization-aware training.
However, one crucial aspect of FP4, that has been overlooked by these proposals, is the redundant negative zero encoding. Due to the inherent sign-magnitude representation, FP4 contains both positive and negative zeroes in its quantization values, despite one being redundant. In this post, we discuss how to intelligently repurpose this redundant zero as an additional, meaningful quantization value, which improves model accuracy compared to the basic FP4 format.
Recap of FP4
We briefly discuss the concept of FP4, MXFP4, and NVFP4, which are illustrated in Figure 1.
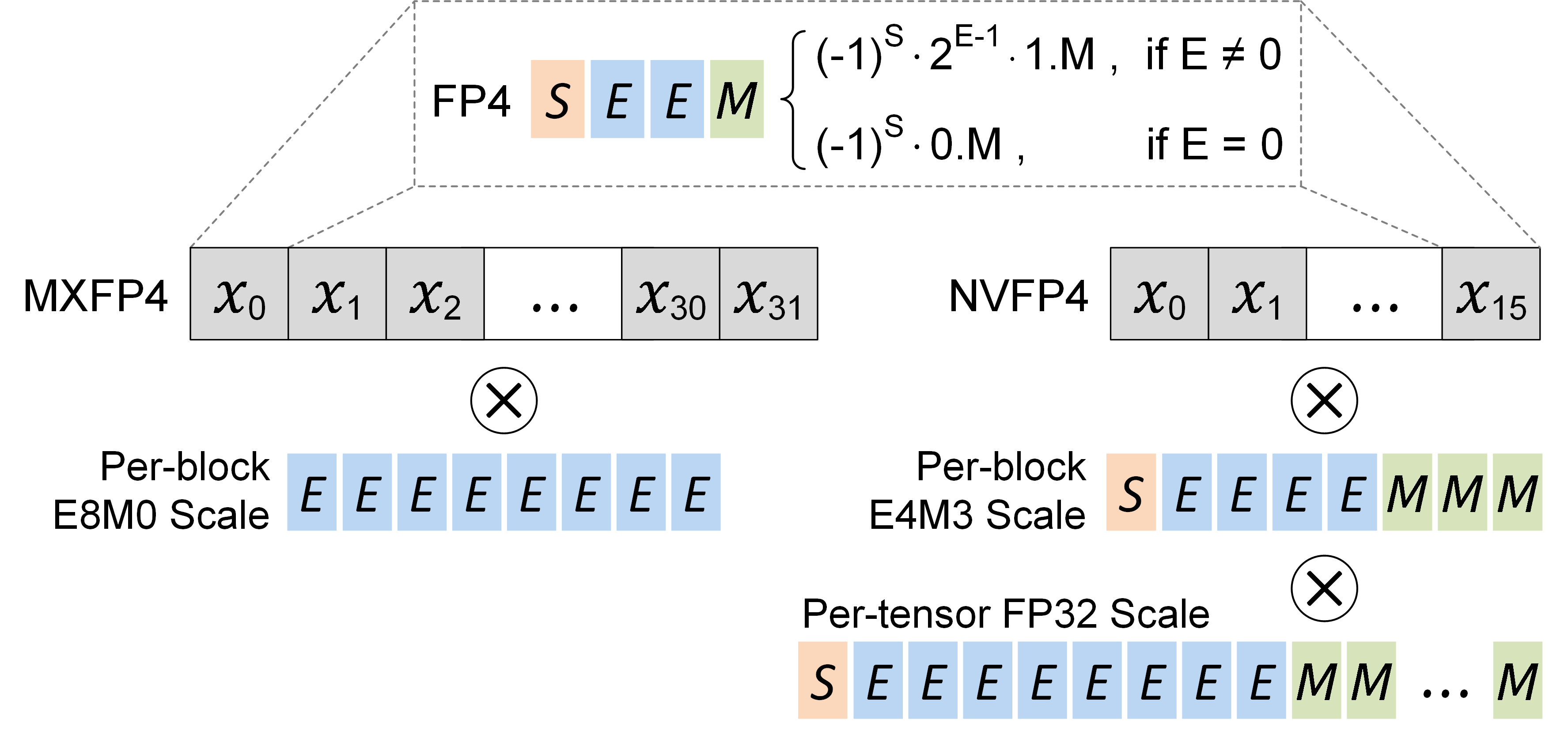
Definition
According to the OCP standard, the FP4 format contains 1 sign bit, 2 exponent bit, and 1 mantissa bits. It can represent 15 quantization values [0, ±0.5, ±1.0, ±1.5, ±2.0, ±3.0, ±4.0, ±6.0].
Microscaling FP4 (MXFP4)
According to the OCP standard, the microscaling (MX) format specifies that a block of 32 elements shares an E8M0 scale factor, which is an unsigned representation of the conventional FP32 exponent. After scaling, each element is quantized to a specified data type, e.g., FP4.
NVIDIA FP4 (NVFP4)
The latest NVIDIA Blackwell GPU architecture introduces the NVFP4 format, which differs from MXFP4 in two aspects. First, it reduces the quantization block size from 32 to 16, enabling finer-grained scaling than MXFP4. Second, it adopts a two-level scaling approach, where every block of 16 elements share an FP8-E4M3 scale factor, followed by an FP32 scale factor shared per tensor.
Redundant Zero Remapping (RaZeR)
One disadvantage of FP4 comes from its inherent sign-magnitude representation that introduces both positive and negative zeroes, despite one of them being redundant. In other words, the standard FP4 format wastes 1/16 = 6.25% of the available encoding. To address this, we propose Redundant Zero Remapping (RaZeR), originally published in our HPCA 2025 paper. RaZeR allows the negative zero encoding to be replaced by one of some pre-defined special values (SVs), resulting in an extended set of quantization values: [SV, 0, ±0.5, ±1.0, ±1.5, ±2.0, ±3.0, ±4.0, ±6.0]. Ideally, the SV may contain arbitary value, e.g., anything from FP16. But computing such a high-precision SV will incur considerable hardware overhead and offset the energy efficiency brought by FP4. Hence, we limit the choices of SV to fixed-point values with one fraction bit, i.e., an multiple of 0.5 as in FP4. Figure 2 illustrates an example design of RaZeR, which allows the negative zero to be remapped to six SVs: [±2.5, ±5.0, ±8.0].
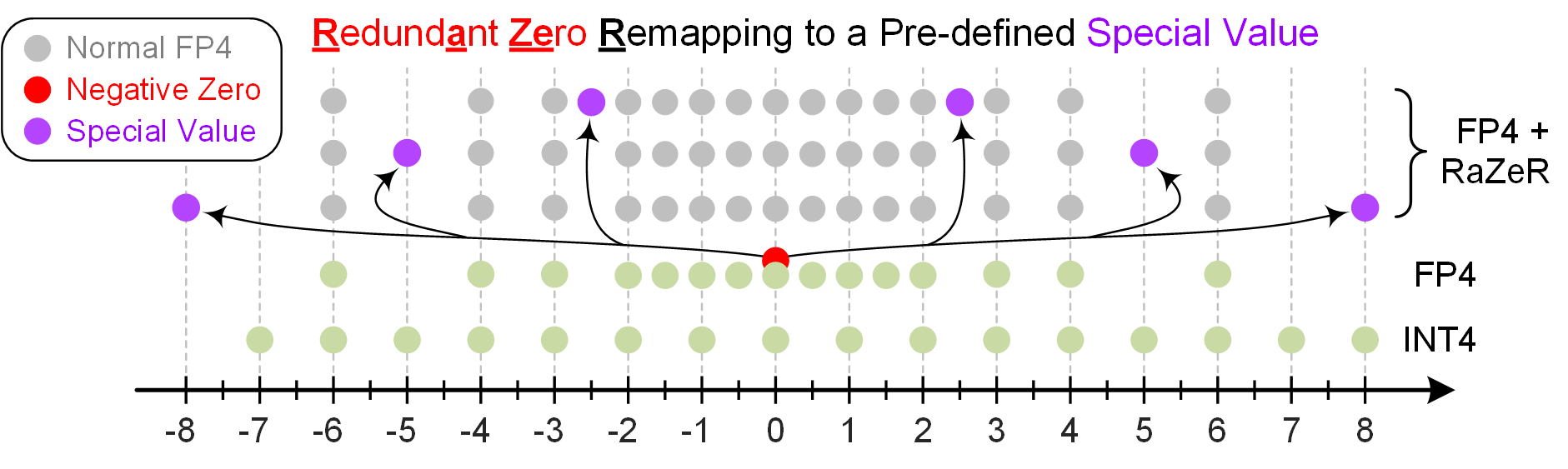
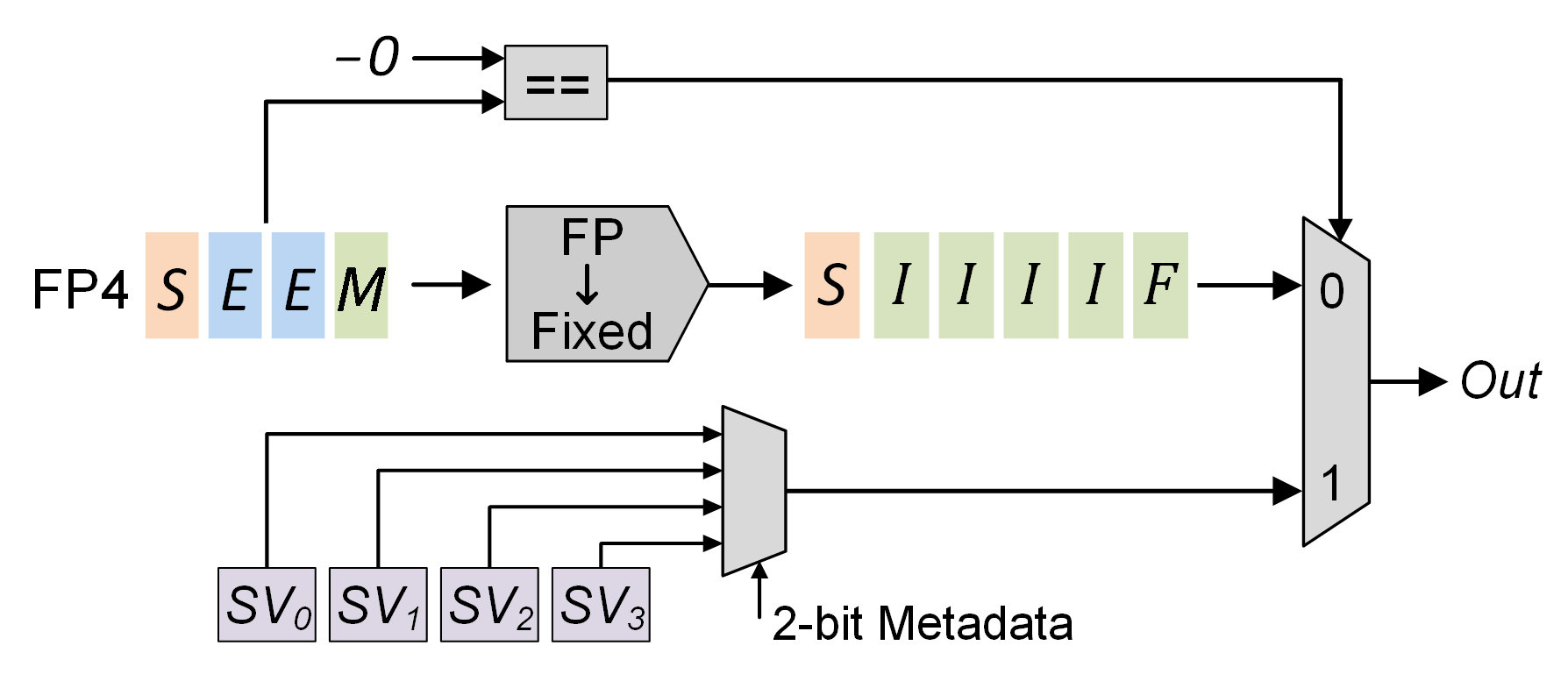
In order to integrate RaZeR with MXFP4 and NVFP4, each block of elements can adaptively select its own optimal SV. Specifically, the quantization algorithm can iterate over all pre-defined SVs for a block, and selects the SV that minimizes the block’s resulting quantization error. To identify which SV is selected, each block stores a logN-bit metadata, where N is the number of pre-defined SVs. In addition, a lightweight hardware decoder is required to perform computation with RaZeR, as illustrated in Figure 3. Assume there are four pre-defined SVs stored in dedicated registers, which are indexed via a 2-bit metadata. During computation, the FP4 operand is compared with negative zero, and if equal, the target SV associated with the current quantization block will be output.
Experiment Results
To demonstrate the benefits of RaZeR, we implement six weight-only quantization functions to evaluate the impact of FP4, MXFP4, NVFP4, FP4-RaZeR, MXFP4-RaZeR, and NVFP4-RaZeR. For RaZeR, we choose four pre-defined SVs: [±5.0, ±8.0]. Both FP4 and FP4-RaZeR adopt a block size of 128 with a per-block FP16 scale factor. While MXFP4-RaZeR and NVFP4-RaZeR use the same block size and scaling configuration as MXFP4 and NVFP4, respectively. The code to reproduce our experiments is available here.
The table below shows the perplexity of Wikitext2 and C4 datasets across a range of LLMs, all using the instruction-tuned versions. A lower perplexity indicates better model performance. Th results demonstrate that adding RaZeR consistently outperforms FP4, MXFP4, and NVFP4.
| Method |
Block Size |
Scale Format |
Llama-3.1-8B | Llama-3.2-3B | QWen2.5-3B | QWen2.5-7B | QWen2.5-14B | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Wiki2 | C4 | Wiki2 | C4 | Wiki2 | C4 | Wiki2 | C4 | Wiki2 | C4 | |||
| FP16 |
N/A |
N/A |
7.21 |
10.38 |
11.05 |
14.48 |
8.56 |
12.03 |
7.46 |
10.88 |
5.69 |
9.38 |
| FP4 |
128 |
FP16 |
7.71 |
11.15 |
11.98 |
15.53 |
9.27 |
12.91 |
7.79 |
11.31 |
6.17 |
9.72 |
| FP4-RaZeR |
128 |
FP16 |
7.60 |
10.97 |
11.94 |
15.40 |
9.11 |
12.71 |
7.79 |
11.20 |
6.14 |
9.68 |
| MXFP4 |
32 |
E8M0 |
8.14 |
11.60 |
12.31 |
16.01 |
9.44 |
13.09 |
8.48 |
11.97 |
6.41 |
9.89 |
| MXFP4-RaZeR |
32 |
E8M0 |
7.68 |
11.01 |
11.76 |
15.31 |
9.14 |
12.80 |
7.77 |
11.25 |
6.22 |
9.70 |
| NVFP4 |
16 |
E4M3 + FP32 |
7.56 |
10.93 |
11.73 |
15.15 |
9.12 |
12.60 |
7.73 |
11.13 |
6.05 |
9.63 |
| NVFP4-RaZeR |
16 |
E4M3 + FP32 |
7.42 |
10.71 |
11.41 |
14.89 |
8.95 |
12.45 |
7.67 |
11.05 |
5.95 |
9.56 |
Related Work
Although the focus of RaZeR is to address the redundant zero encoding of FP4, there is a recent work, BlockDialect, that configures the two largest magnitude values of FP4 to capture various large magnitude distributions. In the meanwhile, most of the small magnitude values to remain consistent with FP4, reducing the hardware complexity to support diverse encodings. The proposed RaZeR is synergistic to BlockDialect.
Conclusion
In this post, we introduce RaZeR, which adaptively remaps the redundant zero encoding of FP4 to an additional, meaningful quantization value. We empirically validate that RaZeR significantly improves model accuracy compared to FP4, MXFP4, and NVFP4. This provides a guidance for future FP4 tensor core design.
Citing
@misc{abdelfattah2025_razer_blog,
title={Extending MXFP4 and NVFP4 with Redundant Zero Remapping (RaZeR) for Accurate 4-bit LLM Quantization},
author={Yuzong Chen and Xilai Dai and Mohamed Abdelfattah},
year={2025},
url={https://abdelfattah-lab.github.io/blog/razer_blog},
}





